tl;dr This short blog post serves to me to recollect some of the thing I have been learning (climbing)
about Elliptic Curves Cryptography (ECC from now on) during the last
months/years, so please take it with a grain of salt since it might
contains some erroneous beliefs.
'80 - Introduction
Giambattista Vico
was an Italian political philosopher and rhetorician, historian and
jurist, of the Age of Enlightenment famous (also) for the concept of
historical courses and resorts. This can be resumed with: "some events are repeated in the same way even after a long time; and this is not by chance". Well it seems that this might also applies to ECC so he maybe he was right :)
Elliptic Curve made its first appearance in cryptography with Lenstra in 1984 (eventually published in 1987). Curiously enough he introduced them not while trying to come up with a new crypto system but he employed EC in order to factor integers (a side note, there is a really beautiful survey about the number factorization problem by the great Carl Pomerance). Then it did not take long for Neal Koblitz and independently (as often happens in science) Victor S. Miller to connects the dots and coming with a brand new crypto system that translated the Diffie Hellman technique from finite field to EC. Clearly the main advantage claimed back then (and it looks that this still stands 30 years later) is that EC are immune to index-calculus attacks.
Great starting points to learn ECC are :
that are so called Weierstrass curves. This is a really classic shape of elliptic curve.
Elliptic Curve made its first appearance in cryptography with Lenstra in 1984 (eventually published in 1987). Curiously enough he introduced them not while trying to come up with a new crypto system but he employed EC in order to factor integers (a side note, there is a really beautiful survey about the number factorization problem by the great Carl Pomerance). Then it did not take long for Neal Koblitz and independently (as often happens in science) Victor S. Miller to connects the dots and coming with a brand new crypto system that translated the Diffie Hellman technique from finite field to EC. Clearly the main advantage claimed back then (and it looks that this still stands 30 years later) is that EC are immune to index-calculus attacks.
Great starting points to learn ECC are :
- Dan Boneh's video Cryptography: From Mathematical Magic to Secure Communication
- Nick Sullivan's A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography
- Andrea Corbellini's series Elliptic Curve Cryptography: finite fields and discrete logarithms
'90 - ECC NIST Standard
Fast forward to the '90s when NIST standardized some EC. The EC in the standard were in the form
y^2 = ax^3 + ax + b
that are so called Weierstrass curves. This is a really classic shape of elliptic curve.
 |
| Weierstrass curve |
The
formulas used for this curves are derived from the work done by the
Chudnovsky brothers and as we will see shortly might not be the most
efficient. The complete formulas are somehow complicated and on top is
not easy to implement constant time algorithm for those curves (unless
replace all that code with curve specific, constant-time code). This paper from Brown,Hankerson, Lopez, Menezes shows several optimizations that can be done for NIST's elliptic curves.
One important thing to remember for the sake of this blog post is that this kind of curves have a minimum cofactor of 1, hence the might have a prime order (like all the NIST curves).
One thing to take care when implementing EC is to employ point validation, in order to avoid invalid curve attacks (see the recent Critical vulnerability in JSON Web Encryption for an example ).
So far so good. For many years did not gain too much popularity among the practitioners, probably due patent related worryings.
But as this wasn't still enough goodies, as djb explains in the The first 10 years of Curve25519 talk, while him and Tanja moved in the Netherlands they discovered Edwards (and twisted Edwards) curves.
And they immediately got the idea to employ those new object for signing starting from Schnorr signature (this became eventually the Ed25519 signature system). Now it turns out that every Montgomery Curve is bi-rationally equivalent to a twisted Edward curve (in particular: Curve25519).
Beautiful, right? Yes indeed but but but ... there is a little caveat: Montgomery Curves have a minimum cofactor of 4 (Curve 25519 has cofactor 8). We will see shortly how this is relevant...
Second we started to see some catastrophic failures (about 1.000.000 $!!!!!) related to curve having cofactor > 1 (is also true that CryptoNote employed a rather exotic flow without a proper understanding of the underlying primitive, but still).
It appears clearly that what it seems to be a settled (by djb et al) problem is actually not (at all).
Lately the curve mailing list is full of discussion about:
and as Isis says in another curve mailing list thread: "... To say that cofactors are annoying would be putting it mildly! ..".
'00 - DJB curves
In 2006 djb published the famous Curve25519 paper. In this work he leverages some work done by Montgomery, the so called (unsurprisingly) Montgomery curve. A Montgomery curve comes in the form:
by^2 = x^3 + ax^2 + x
A Montgomery curve is different from the usual Weierstrass form:
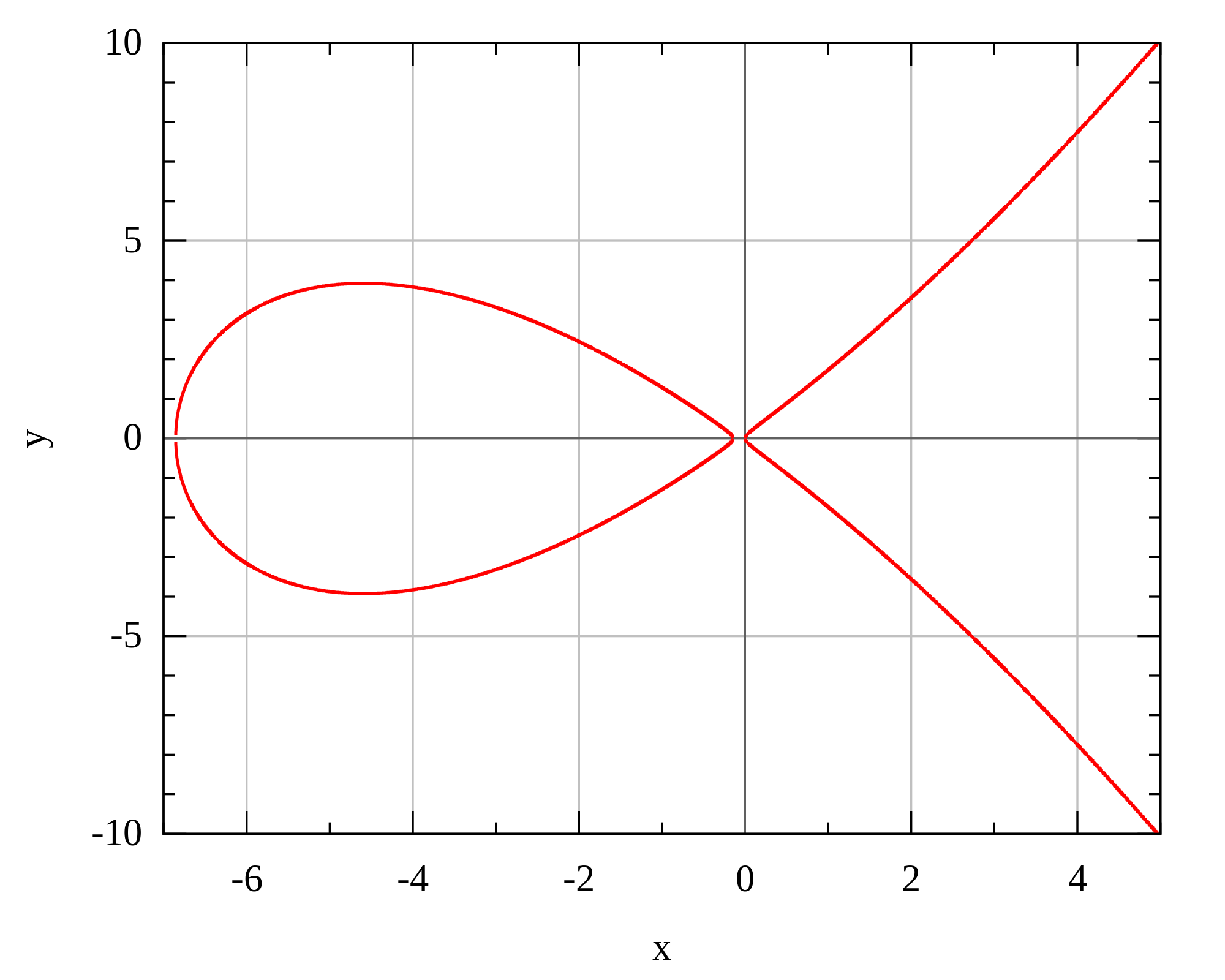 |
| Montgomery curve |
but it turns out that constitute ≈25% of all elliptic curves. The main advantages of using such curve shapes are:
- Speed: a single scalar multiplication is very simple and fast (it can leverage the so called Montgomery Ladder)
- Side-channel resistance: the Montgomery Ladder is not only fast but is also side-channel resistant,
- Security: one peculiarity of Montgomery Ladder is that the output is guaranteed to be either on the curve or on its twist. So if a curve is chosen to be twist secure there is no risk to fall into the invalid curve trap seen above.
But as this wasn't still enough goodies, as djb explains in the The first 10 years of Curve25519 talk, while him and Tanja moved in the Netherlands they discovered Edwards (and twisted Edwards) curves.
 |
| Edward curve |
And they immediately got the idea to employ those new object for signing starting from Schnorr signature (this became eventually the Ed25519 signature system). Now it turns out that every Montgomery Curve is bi-rationally equivalent to a twisted Edward curve (in particular: Curve25519).
Beautiful, right? Yes indeed but but but ... there is a little caveat: Montgomery Curves have a minimum cofactor of 4 (Curve 25519 has cofactor 8). We will see shortly how this is relevant...
'10 - Historical courses and resorts
Gradually
ECC was better understood (also some patents expired) and ECC grew up
popularity together (also) within mobile devices (EC arithmetic is way
faster since it uses way less bits). Also the majority of TLS
connections are now served using ECDHE (we probably need to thank Snowden for this). Together with EC also djb curves gain more and more popularity mainly due to two reasons:
- Curve 25519 has all the goodies listed above
- People have more confidence on djb than NIST
Second we started to see some catastrophic failures (about 1.000.000 $!!!!!) related to curve having cofactor > 1 (is also true that CryptoNote employed a rather exotic flow without a proper understanding of the underlying primitive, but still).
It appears clearly that what it seems to be a settled (by djb et al) problem is actually not (at all).
Lately the curve mailing list is full of discussion about:
and as Isis says in another curve mailing list thread: "... To say that cofactors are annoying would be putting it mildly! ..".
Now I am not saying this is the end of Curve25519 and/or Montgomery Curve BUT lately the great Prof. Barreto proposed a new curve that is prime order and a Weierstrass curve.
This made me thinking, is Prof. Barreto right? Should we go back to Weierstrass curves? Aka ending as we started with Vico

Comments